Example: PID Design method for the Pitch Controller
Proportional control
Proportional-Derivative control
Proportional-Integral-Derivative control
In the Pitch Controller Modeling page, the transfer function was derived as
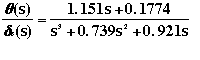
The input (elevator deflection angle, delta e) will be 0.2 rad (11 degrees), and the output is the pitch angle
(theta).
The design requirements are
- Overshoot: Less than 10%
- Rise time: Less than 2 seconds
- Settling time: Less than 10 seconds
- Steady-state error: Less than 2%
To see the original problem setup, please refer to the Pitch Controller Modeling page.
Recall from the PID Tutorial page, the transfer function of a PID controller is:
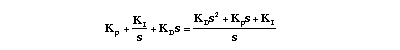
We will implement combinations of proportional (Kp), integral (Ki), and derivative (Kd) controllers in an unity feedback
system shown below to study the system output.
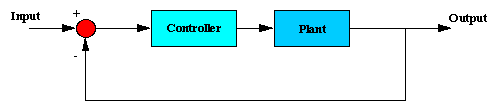 Let's first take a look at a proportional control.,
Let's first take a look at a proportional control.,
Proportional control
The first thing in solving this problem using PID control is to find a closed-loop transfer function with a
proportional control (Kp). A closed-loop transfer function can be obtained either by hand or using the Matlab function
called cloop. Either way, you should obtain the closed-loop transfer function
as:

Note: Matlab cannot manipulate symbolic variables. To use the function cloop, enter the following commands to an m-file and run it in
the Matlab command window. You should obtain the numerical coefficients of numerator and denominator of the closed-loop
transfer function.
Kp=[1]; %Enter any numerical value for the proportional gain
num=[1.151 0.1774];
num1=conv(Kp,num);
den1=[1 0.739 0.921 0];
[numc,denc]=cloop (num1,den1)
For now, let the proportional gain (Kp) equal 2 and observe the system behavior.
We will use the closed-loop transfer function derived by
hand. Enter the following commands into a new m-file and run it in the Matlab command
window. You should obtain the step response similar to the one shown below:
de=0.2;
Kp=2;
numc=Kp*[1.151 0.1774];
denc=[1 0.739 1.151*Kp+0.921 0.1774*Kp];
t=0:0.01:30;
step (de*numc,denc,t)

As you see, both the overshoot and the settling time need some improvement.
PD control
Recall from the PID Tutorial page, the derivative controller will reduce both
the overshoot and the settling time. Let's try a PD controller. The closed-loop transfer function of the system with a
PD controller is:

Using the commands shown below and with several trial-and-error runs, a proportional gain (Kp) of 9 and a derivative gain
(Kd) of 4 provided the reasonable response. To comfirm this, change your m-file to the following and run it in the Matlab command
window. You should obtain the step response similar to the one shown below:
de=0.2;
Kp=9;
Kd=4;
numc=[1.151*Kd 1.151*Kp+0.1774*Kd 0.1774*Kp];
denc=[1 0.739+1.151*Kd 0.921+1.151*Kp+0.1774*Kd 0.1774*Kp];
t=0:0.01:10;
step (de*numc,denc,t)

This step response shows the rise time of less than 2 seconds, the overshoot of less than 10%, the settling time of
less than 10 seconds, and the steady-state error of less than 2%. All design requirements are satisfied.
PID Control
Even though all design requirements were satisfied with the PD controller, the integral controller (Ki) can be
added to
reduce the sharp peak and obtain smoother response.
After several trial-and-error runs, the proportional gain (Kp) of 2, the integral gain (Ki) of 4, and the derivative gain (Kd)
of 3 provided smoother step response that still satisfies all design requirements. To cofirm this, enter the
following commands to an m-file and run it in the command window. You should obtain the step response shown below:
Note: This time we are going to use the function cloop
to find the closed-loop transfer function, and then obtain the step response.
de=0.2;
Kp=2;
Kd=3;
Ki=4;
numo=[1.151 0.1774];
deno=[1 0.739 0.921 0];
numpid=[Kd Kp Ki];
denpid=[1 0];
num1=conv(numo,numpid);
den1=conv(deno,denpid);
[numc,denc] = cloop(num1,den1);
t=0:0.01:10;
step (de*numc,denc,t)

Comments
- To find appropriate gains (Kp, Kd, and Ki), you can use the table shown in
PID Tutorial page; however, please keep in your mind that changing one gain might change
the effect of the other two. As a result, you may need to change other two gains as you change one gain.
- Our system with a PI controller do not provide the desired response;
thus, a PI Control section was omitted from this page.
You may confirm this by using the m-file shown in PID Control section, and set Kd equals to zero.
User feedback
PID Examples
Cruise Control |
Motor Speed |
Motor Position |
Bus Suspension |
Inverted Pendulum |
Pitch Control |
Ball and Beam
Pitch Control Examples
Modeling |
PID |
Root Locus |
Frequency Response |
State Space |
Digital Control: SS
Tutorials
Basics |
Modeling |
PID |
Root Locus |
Frequency Response |
State Space |
Digital Control |
Examples



8/26/97 DK

