

|
|
Train system
Free body diagram and Newton's law
State-variable and output equations
Matlab representation
Matlab can be used to represent a physical system or a model. To begin with, let's start with a review of how to represent a physical system as a set of differential equations.
In this example, we will consider a toy train consisting of an engine and a car. Assuming that the train only travels in one direction, we want to apply control to the train so that it has a smooth start-up and stop, along with a constant-speed ride.
The mass of the engine and the car will be represented by M1 and M2, respectively. The two are held together by a spring, which has the stiffness coefficient of k. F represents the force applied by the engine, and the Greek letter, mu (which will also be represented by the letter u), represents the coefficient of rolling friction.

The system can be represented by following Free Body Diagrams.
From Newton's law, you know that the sum of forces acting on a mass equals the mass times its acceleration. In this case, the forces acting on M1 are the spring, the friction and the force applied by the engine. The forces acting on M2 are the spring and the friction. In the vertical direction, the gravitational force is canceled by the normal force applied by the ground, so that there will be no acceleration in the vertical direction. The equations of motion in the horizontal direction are the followings:
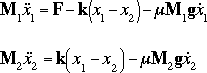
This set of system equations can now be manipulated into state-variable form. Knowing state-variables are X1 and X2 and the input is F, state-variable equations will look like the following:
Let the output of the system be the velocity of the engine. Then the output equation will become:
To find the transfer funciton of the system, first, take Laplace transforms of above state-variable and output equations.
Using these equations, derive the transfer function Y(s)/F(s) in terms of constants. When finding the transfer function, zero initial conditions must be assumed. The transfer function should look like the one shown below.
Another method to solve the problem is to use the state-space form. Four matrices A, B, C, and D characterize the system behavior, and will be used to solve the problem. The state-space form that were manipulated from the state-variable and the output equations is shown below.
Now we will show you how to enter the equations derived above into an m-file for Matlab. Since Matlab can not manipulate symbolic variables, let's assign
numerical values to each of the variables. Let
Create an new m-file and enter the following commands.
Now you have one of two choices: 1) Use the transfer function, or 2) Use the state-space form to solve the problem. If you choose to use the transfer function, add the following commands onto the end of the m-file which you have just created.
num=[M2 M2*u*g 1]; den=[M1*M2 2*M1*M2*u*g M1*k+M1*M2*u*u*g*g+M2*k M1*k*u*g+M2*k*u*g];
If you choose to use the state-space form, add the following commands at the end of the m-file, instead of num and den matrices shown above.
A=[ 0 1 0 0;
-k/M1 -u*g k/M1 0;
0 0 0 1;
k/M2 0 -k/M2 -u*g];
B=[ 0;
1/M1;
0;
0];
C=[0 1 0 0];
D=[0];
See the Matlab basics tutorial to learn
more about entering matrices.
This tutorial contain seven examples which allows you to learn more about modeling. You can link to them from below.