Problem Setup
System Equations
Matlab Representation and Open-Loop Response

Problem Setup

A ball is placed on a beam, see figure below, where it is allowed to roll with 1 degree of freedom along the length of the beam. A lever arm is attached to the beam at one end and a servo gear at the other. As the servo gear turns by an angle theta, the lever changes the angle of the beam by alpha. When the angle is changed from the vertical position, gravity causes the ball to roll along the beam. A controller will be designed for this system so that the ball's position can be manipulated.

For this problem, we will assume that the ball rolls without slipping and friction between the beam and ball is negligible. The constants and variables for this example are defined as follows:

The design criteria for this problem are:

• Settling time less than 3 seconds
• Overshoot less than 5%

System Equations

The Lagrangian equation of motion for the ball is given by the following:

1. Transfer Function

Rearranging we find the transfer function from the gear angle (theta(s)) to the ball position (R(s)).

It should be noted that the above plant transfer function is a double integrator. As such it is marginally stable and will provide a challenging control problem.

2. State-Space

However, for our state-space example we will be using a slightly different model. The same equation for the ball still applies but instead of controlling the position through the gear angle, theta, we will control alpha-doubledot. This is essentially controlling the torque of the beam. Below is the representation of this system:

Note: For this system the gear and lever arm would not be used, instead a motor at the center of the beam will apply torque to the beam, to control the ball's position.

Matlab Representation and Open-Loop Response

1. Transfer Function

m = 0.111;
R = 0.015;
g = -9.8;
L = 1.0;
d = 0.03;
J = 9.99e-6;

K = (m*g*d)/(L*(J/R^2+m));   %simplifies input

num = [-K];
den = [1 0 0];
printsys(num,den)

num/den = 

           0.21
        ----------
           s^2

step(0.25*num,den)

You should see the following plot showing the balls position as a function of time:

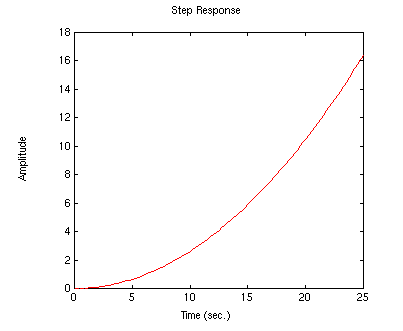
From this plot it is clear that the system is unstable in open-loop causing the ball to roll right off the end of the beam. Therefore, some method of controlling the ball's position in this system is required. Three examples of controller design are listed below for the transfer function problem. You may select from PID, Root Locus, and Frequency Response.

2. State-Space

m = 0.111;
R = 0.015;
g = -9.8;
J = 9.99e-6;

H = -m*g/(J/(R^2)+m);
   
A=[0 1 0 0
   0 0 H 0
   0 0 0 1
   0 0 0 0];
B=[0;0;0;1];
C=[1 0 0 0];
D=[0];

step(A,B*.25,C,D)

Like the plot for the transfer function this plot shows that the system is unstable and the ball will roll right off the end of the beam. Therefore, we will require some method of controlling the ball's position in this system. The State-Space example below shows how to implement a controller for this type of system.

If you are interested in knowing how to convert state-space representations to transfer function representations, and vice versa, please refer to the Conversions page.

Modeling Examples

Cruise Control | Motor Speed | Motor Position | Bus Suspension | Inverted Pendulum | Pitch Controller | Ball and Beam

Ball & Beam Examples

Modeling | PID | Root Locus | Frequency Response | State Space | Digital Control

Tutorials

Basics | Modeling | PID | Root Locus | Frequency Response | State Space | Digital Control | Examples