Digital Control Example: Ball and Beam problem using PID
Control
Digital PID controller
Discrete transfer function
Open-loop response
Proportional control
Proportional-Derivative control
In this digital control version of the ball and beam experiment, we are going to use the PID control method
to design the digital controller. If you refer to the Ball and Beam Modeling page, the
open-loop transfer function was derived as
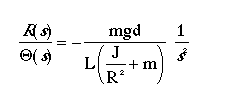
| m | mass of the ball | 0.11 kg |
| g | gravitational acceleration | 9.8 m/s^2 |
| d | lever arm offset | 0.03 m |
| L | length of the beam | 1.0 m |
| R | radius of the ball | 0.015 m |
| J | ball's moment of inertia | 9.99e-6 kgm^2 |
| R(s) | ball position coordinate (m) | |
| theta(s) | servo gear angle | 0.25 rad |
The design criteria for this problem are:
- Settling time less than 3 seconds
- Overshoot less than 5%
Digital PID controller
If you refer to any of the PID control problem for continuous systems, the PID transfer function was expressed
as

As you noticed the above transfer function was written in terms of s. For the digital PID control,
we use the following transfer function in terms of z.

Discrete transfer function
The first thing to do here is to convert the above continuous system transfer function to discrete transfer
function. To do this, we are going to use the Matlab function called c2dm. To use this c2dm, we
need to specify four arguments: numerator and denominator matrices, sampling time (Ts), and the 'method'. You
should already be familiar with how to enter numerator and denominator matrices. The sampling time should be
smaller than 1/(30*BW) sec, where BW is the closed-loop bandwidth frequency. The method we will use is the
zero-order hold ('zoh').
Assuming that the closed-loop bandwidth frequency is around 1 rad/sec, let the sampling time be 1/50
sec/sample. Now we are ready to use c2dm. Enter the following commands to
an m-file.
m = 0.111;
R = 0.015;
g = -9.8;
L = 1.0;
d = 0.03;
J = 9.99e-6;
K = (m*g*d)/(L*(J/R^2+m)); %simplifies input
num = [-K];
den = [1 0 0];
Ts = 1/50;
[numDz,denDz]= c2dm (num,den,Ts,'zoh')
Running this m-file in the Matlab command window gives you the following matrices.
numDz =
1.0e-0.4 *
0 0.4200 0.4200
denDz =
1 -2 1
From these matrices, the discrete transfer function can be written as

Open-loop response
Now we will observe the ball's response to a step input of 0.25 m. To do this, enter the following commands to
an new m-file and run it in the command window. You should see the following response.
numDz = 0.0001*[0.42 0.42];
denDz = [1 -2 1];
[x] = dstep (0.25*numDz,denDz,251);
t=0:0.02:5;
stairs(t,x)

From this plot, it is clear that the open-loop system is unstable causing the ball to roll off from the end
of the beam.
Proportianal Control
Now we will add the proportional control (Kp) to the system and obtain the closed-loop system response. For
now let Kp equal to 100 and see what happens to the response. Enter the following commands to an new
m-file and run it in the command window.
numDz = 0.0001*[0.42 0.42];
denDz = [1 -2 1];
Kp=100;
[numDzC,denDzC]=cloop (Kp*numDz,denDz);
[x] = dstep (0.25*numDzC,denDzC,251);
t=0:0.02:5;
stairs(t,x)

As you can see, the addition of proportional control does not make the system stable. You may try to increase
the proportional gain (Kp) and confirm that the system remains unstable.
Proportional-Derivative control
Now we will add a derivative term to the controller. Keep the proportional gain (Kp) equal to 100, and let
the derivative gain (Kd) equal to 10. Copy the following code to an new m-file and run it to view the system
response.
numDz = 0.0001*[0.42 0.42];
denDz = [1 -2 1];
Kp=100;
Kd=10;
numpd = [Kp+Kd -(Kp+2*Kd) Kd];
denpd = [1 1 0];
numDnew = conv(numDz,numpd);
denDnew = conv(denDz,denpd);
[numDnewC,denDnewC] = cloop(numDnew,denDnew);
[x] = dstep (0.25*numDnewC,denDnewC,251);
t=0:0.02:5;
stairs(t,x)

Now the system is stable, but the rise time is too long. From the PID
Tutorial page, we see that the increasing the proportional gain (Kp) will decrease the rise time. Let's
increase the proportional gain (Kp) to 1000 and see what happens. Change Kp in the above m-file from
100 to 1000 and rerun it in the command window. You should see the following step response.

As you can see, all of the design requirements are satisfied. For this particular problem, no
implementation of an integral control was needed. But remember there is more than
one solution for a control problem. For practice, you may try different P, I and D combinations to obtain
a satisfactory response.
User Feedback
Digital Control Examples
Cruise Control: RL |
Motor Speed:PID |
Motor Position:RL |
Bus Suspension: SS |
Inverted Pendulum:SS |
Pitch Controller: SS |
Ball and Beam:PID
Ball & Beam Examples
Modeling |
PID |
Root Locus |
Frequency Response |
State Space |
Digital Control
Tutorials
Basics |
Modeling |
PID |
Root Locus |
Frequency Response |
State Space |
Digital Control |
Examples



8/25/97 DK

