6. Two Complex Poles - the Lowpass Form

This section highlights second order systems with complex poles and no zeros. The absence of zeros allows a non-zero steady state response to a step input. The sketches below show a couple of systems that are described by such a transfer function. They both have more than one form of energy storage (capacitive and inductive, spring and mass), which is a characteristic feature of passive systems with complex poles. In the mechanical system, the output is displacement of the mass in response to displacement of the spring/damper assembly. They both have a non-zero steady state response to a step input.

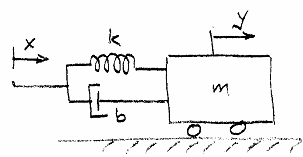
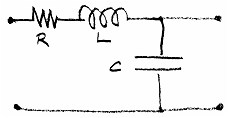
If they are lightly damped (i.e., little power lost in the dissipative elements compared with power flow in the storage elements), then these systems can resonate. The animations will show this behaviour. However, if such systems are part of a design, rather than something provided by nature, then it is more common not to make them strongly resonant. Instead, we use the fact of non-zero DC gain, and set them up just slightly underdamped, in order to make a good lowpass filter.

where p₁ and p₂ are the two poles and there are no zeros. Since complex poles occur in conjugate pairs, we can characterize them by two real parameters, such as the real and imaginary parts of one of them. We will use two common ways to describe the pole locations: natural frequency w_o & damping factor z, and real part s₁ & imaginary part w₁. We are interested in complex poles, so they look like this:

We'll see two set of animations: one set for the w_o, z parameterization and one for the s₁, w₁ parameterization. In each case, we'll hold one of the variables constant and sweep the other.

First, fix the natural frequency w_o at 1 rad/sec and sweep the damping factor z from a positive value down to zero (we won't bother with negative values, which give unstable systems). Click here to see the animation and leave the animation window open as you read this section. Drag the slider back and forth with your mouse to get different parameter values. You can see that, for complex poles, w_o is the pole radius (constant at 1) and z is the sine of the angle between the pole and the imaginary axis.

When the poles are real (z > 1), we have the system with two real poles that we investigated in Section 4 , so there is nothing new. When they start to move out on the circle (complex poles), it gets more interesting, as oscillations show up in the time responses, and resonance can be seen in the frequency responses. The time constant is the negative reciprocal of the real part of the pole locations (t = -1/(zwo)) and the oscillation frequency (the damped natural frequency) is the imaginary part of the pole locations (w_d = sqrt(1-z²)w_o). Evidently, z controls the overall shape of the response.

For small values of z, there are many oscillations in the time response. This condition is termed resonance, and the number of oscillations per time constant is determined solely by z. In resonant conditions, the interesting action in the frequency responses (both magnitude and phase) is confined to a narrow region around the resonant frequency. The oscillation frequency (the damped natural frequency w_d) approaches the natural frequency w_o.

Next, fix the damping factor z at 0.25 and sweep the natural frequency w_o from 0.1 out to 1.4 rad/sec. Click here to see the animation, and drag the slider back and forth with your mouse to get different parameter values. You can see that, as the pole radius w_o increases, the poles move out along a radial line with angle determined by z (the sine of the angle between the pole and the imaginary axis).

Unlike z, the natural frequency w_o does not affect the general shape of the responses. Instead, it acts as a time-frequency scale factor. Increasing w_o expands the scale of the frequency response and of the pole-zero diagram (which is also in the frequency domain). The increase of w_o also compresses the time scale of the step and impulse responses.

First, we will fix the imaginary part w₁ of the first conjugate pole at 1 rad/sec and sweep the real part s₁ from a negative value in to the origin. Click here to see the animated responses and leave the animation window open as you read this section. Drag the slider back and forth with your mouse to get different parameter values.

Since the time constant is the negative reciprocal of the real part of the poles (t = -1/s₁), we see that the effect of changing s₁ with a constant w₁ is simply to change the time constant. The oscillation frequency (the damped natural frequency w_d, which also equals w₁) remains constant.

Finally, we fix the real part s₁ of the poles to -0.25 sec^-1 and sweep the imaginary part w₁ from 0.2 rad/sec out to 3 rad/sec. Click here to see the result. Drag the slider back and forth with your mouse to get different parameter values.

In the step and impulse responses, you see that the time constant t does not change (why?), but the oscillation frequency w_d (the damped natural frequency) increases (again, why?).

In the frequency response, you see that the centre frequency increases. However, the bandwidth (which is about 1/(2t)) stays constant, so the changes in amplitude and phase take place over the same range of frequencies, just with a different centre..

This filter has non-zero DC gain, since it has no zeros. Despite the possibility of resonant behaviour, it is not normally used as a bandpass filter. Instead, it is widely used as a lowpass filter when z = 1/sqrt(2) = 0.707. You can see why in the animation if you drag the slider to get z close to 0.707. In the time domain, its step response has a fast rise time with a level of overshoot that is acceptable for most purposes. In the frequency domain, it is "maximally flat"; that is, the magnitude of the frequency response sags very slowly (zero derivatives at DC) with increasing frequency up to the corner frequency. Similarly, the phase shift is almost linear up to the same point. Together, they mean less distortion of a low frequency desired signal and more suppression of unwanted higher frequencies than in the simple one pole lowpass of Section 2 .

The filter with z = 0.707 is known as a "second order Butterworth" filter. Higher order Butterworth filters - flatter in-band and with a faster dropoff in frequency out of band - are generated by placing several poles in an equispaced manner around the left half of the circle.

This type of response is useful in mechanical systems, too. Remember the sketched mechanical system at the top of the page? It can represent a mechanical system with a spring and shock absorbers.

We don't always choose z = 0.707. In electronic and mechanical systems, it is sometimes important not to have overshoot in the response to a step input. Yet it is also important to have a fast response, rather than a sluggish one. A critically damped system - in which the two real poles are equal - equivalently, z = 1 - gives the shortest rise time without overshoot. Try it in the animation.