

|
|
Transfer functions
Root locus design
Lead-lag controller
What happens to the cart's position?
The transfer function of the plant for this problem is given below:
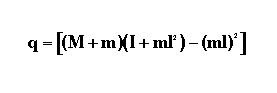
The design criteria (with the pendulum receiving a 1N impulse force from the cart) are:
The rlocus command in Matlab can find the root locus for a system described by state-space equations or by a transfer function. For this problem it will be easier in the long run to use a transfer function (the reason for this will become clear later). The transfer function found from the Laplace transforms for the output Phi (the pendulum's angle) can be set up using Matlab by inputting the numerator and denominator as vectors. Create an m-file (or a '.m' file located in the same directory as Matlab) and copy the following text to model the transfer function:
The control of this problem is a little different than the standard control problems you may be used to. Since we are trying to control the pendulum's position, which should return to the vertical after the initial disturbance, the reference signal we are tracking should be zero. The force applied to the cart can be added as an impulse disturbance. The schematic for this problem should look like the following.
It will be easier to determine the appropriate transfer function to enter into Matlab if we first rearrange the schematic as follows:
Now, we can find the closed-loop transfer function.
This closed-loop transfer function can be modeled in Matlab. The first thing to do is to look at the root locus for the plant by itself, with no compensator. To pick the gain for the proportional control, remember that the settling time has to be less than 5 seconds. This implies that sigma should be more than 4.6/5=0.92. We can put this criteria right on the root locus using the sigrid function, which has to be copied to a m-file. To do this, copy the following code to the end of your m-file (whether your using the transfer function from the Laplace transforms or from the state-space representation):
As you can see, one of the roots of the closed-loop transfer function is in the right-half-plane. This means that the system will be unstable. Look back at the root locus to see why. Part of the root locus lies between the origin and the pole in the right-half-plane. No matter what gain you chose, you will always have a closed-loop pole in this region, making your impulse response unstable. To solve this problem, we need to add another pole at the origin so all the zeros and poles at the origin will cancel each other out and multiple roots will be created in this right-half-plane region. The multiple roots can then be drawn into the left-half-plane to complete the design. Add the following to your m-file:
Now we can begin trying to draw the branches of the root locus into the left half plane. Enter the following two commands into the command window:
This configuration will never have the multiple roots in the left-half-plane. We must reduce the number of asymptotes from three to two by adding one more zero than pole the controller. If just a zero is added, then the intersection of the asymptotes (alpha) would be [(-5.6041+5.5651-0.1428+0+0)-(0+0+z2)]/2. This means the two asymptotes will leave the real axis at roughly -0.1-(1/2)z2. Making z2 as small as possible (assume near the origin) will not pull the multiple roots far enough into the left-half-plane to meet the design requirements (asymptotes will leave at about -0.1).
The solution to this problem is to add another pole far to the left of the other poles and zeros. To keep the right number of asymptotes, another zero should be added as well. The placement of the added pole and zeros is not important except that the pole should be relatively large and the zeros should be relatively small.
Try the m-file below to see what effect the poles and zeros have on the root locus. The polyadd function needs to be copied to the directory you are running Matlab in.
The second plot should be of the same root locus magnified a little so that the root locus around the origin can be seen.
When prompted to pick a location on the root locus, chose a spot on the multiple roots just before they return to the real axis. Your velocity response to the impulse disturbance should look similar to the following:
The response now meets all of the requirements, so no further iteration is needed.
At the beginning on this solution page, the block diagram for this problem was given. The diagram was not entirely complete. The block representing the the position was left out because that part was not being controlled. It would be interesting though, to see what is happening to the cart's position when the controller for the pendulum's angle is in place. To see this, we need to consider the actual system block diagram:
Rearranging a little bit, you get the following block diagram:
The feedback loop represents the controller we have designed for the pendulum. The transfer function from the cart's position to the impulse force, with the feedback controller which we designed, is given as follows:
Recall that den1=den2 if the pole/zero at the origin that was canceled is added back in. So the transfer function from X to F can be simplified to:
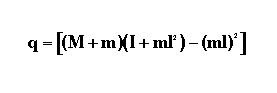
For more about the Laplace transform please refer to the inverted pendulum modeling page.
The pole/zero at the origin canceled out of the transfer function for Phi, has been put back in. So that now den1 = den2, making calculations easier. Now, create a new m-file and run it in the command window:
The top curve represents the pendulum's angle, and the bottom curve represents the cart's position. As you can see, the cart moves, is stabilized at near zero for almost five seconds, and then goes unstable. It is possible that friction (which was neglected in the modeling of this problem) will actually cause the cart's position to be stabilized. Keep in mind that if this is in fact true, it is due more to luck than to anything else, since the cart's position was not included in the control design.
Tutorials