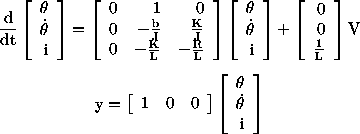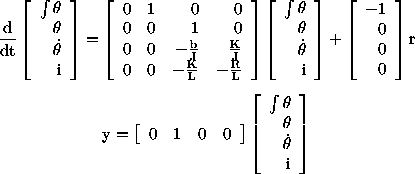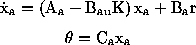Example: A State-Space Controller for DC
Motor Position Control
Designing the full-state feedback controller
Disturbance Response
Adding Integral Action
From the main problem, the dynamic equations in state-space form are the
following:
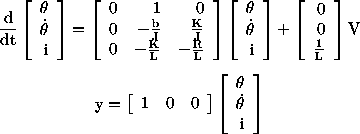
For the original problem setup and the derivation of the above
equations, please refer to the
Modeling DC Motor Position page.
With a 1 rad reference added to the system, the design criteria are:
- Settling time less than 0.04 seconds
- Overshoot less than 16%
- Zero steady-state error to a step input
- Zero steady-state error to a step disturbance
Create a new m-file and type in the
following commands (refer to the main problem for the details of getting
those commands).
J=3.2284E-6;
b=3.5077E-6;
K=0.0274;
R=4;
L=2.75E-6;
A=[0 1 0
0 -b/J K/J
0 -K/L -R/L];
B=[0 ; 0 ; 1/L];
C=[1 0 0];
D=[0];
Designing the full-state feedback controller
Since all of the state variables in our problem are very easy to
measure (simply add an ammeter for current, a tachometer for speed,
and a potentiometer for position), we can design a full-state feedback
controller for the system without worrying about having to add an
observer. The schematic for a full-state feedback system is:
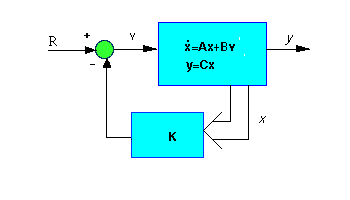
Recall that the characteristic polynomial for this closed-loop system
is the determinant of (sI-(A-BKc)) where s is the Laplace
variable. Since the matrices A and B*Kc are both 3x3
matrices, there should be 3 poles for the system. By designing a
full-state feedback controller, we can move these three poles anywhere
we want them. We shall first try to place them at -100 + 100i and -100-100i
(note that this corresponds to a zeta = 0.5 which gives 0.16%
overshoot and a sigma = 100 which leads to a .04 sec settling time). Once
we come up with the poles we want, Matlab will find the controller
matrix,Kc, for us. Simply add the following code to the end of
your m-file :
p1=-100+100i;
p2=-100-100i;
p3=-200;
Kc=place(A,B,[p1,p2,p3]);
Now look at the schematic above again. We see that after adding the K
matrix into the system, the state-space equations become:
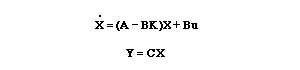
We can see the closed-loop response by simply adding the following line to
the end of your m-file:
t=0:0.001:.05;
step(A-B*Kc,B,C,D,1,t)
Run your m-file in the command window, You should see the following
plot:
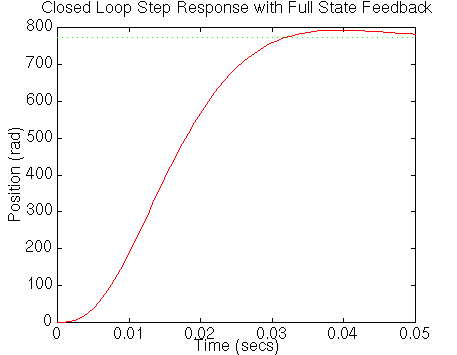
Disturbance Response
In order to get the disturbance response, we must provide the proper
input to the system. Physically, a disturbance is a torque which acts
on the inertia of the motor. A torque acts as an additive term in the
second state equation (which gets divided by J, as do all the other
terms in this equation). We can simulate this simply by modifying our
closed loop input matrix, B, to have a 1/J in the second row. Add
the following line to your m-file and re-run.
step(A-B*Kc,[0;1/J;0],C,D,1,t)
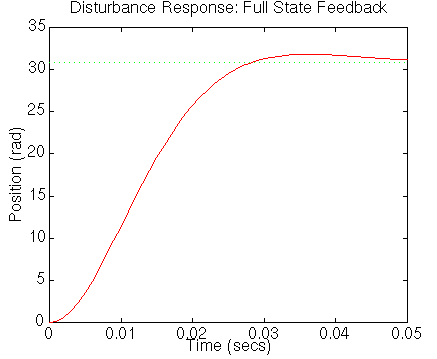
This is not a zero steady-state error to a disturbance, and we will
have to compensate for this.
Adding Integral Action
We know that if we put an extra integrator in series with the plant it
can remove steady-state error to an input. If the integrator comes
before the injection of the disturbance, it will cancel the
disturbance in steady state. This changes our control structure so it
now resembles the following:
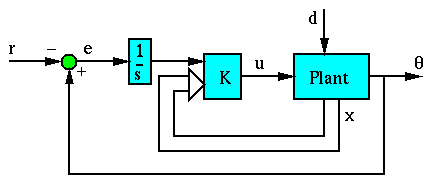
We can model the integrator by augmenting our state equations with an
extra state which is the integral of the output. This adds an extra
equation which states that the derivative of the integral of theta is
theta. This equation will be placed at the top of our matrices. The
input, r, now enters the system before the integrator, so it appears
in the newly added top equation. The output of the system remains the
same.
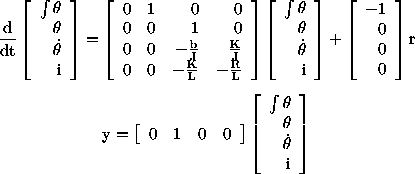
These equations represent the dynamics of the system before the loop
is closed. We will refer to the matrices in this equation as
Aa, Ba, Ca, and Da. We
will refer to the state vector of the augmented system as
xa. Note that the reference, r, does not affect the states
(except the integrator state) or the output of the plant - this is
expected, since there is no path from the reference to the plant
input, u, without implementing the feedback matrix, Kc.
In order to find the closed loop equations, we have to look at how the
input, u, affects the plant. In this case, it is exactly the same as
in the unaugmented equations. Therefore, there is a vector, call it
Bau, which replaces Ba when we are treating u as
the input. This is just our old B vector with an extra zero added as a
first row. Since u=Kc*xa is the input to the plant for the
closed loop, but r is the input to the closed loop system, the closed
loop equations will depend on both Bau and Ba.
The closed loop equations will become:
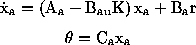
Now, the integral of the output will be fed back, and will be used by
the controller to remove steady state error to a disturbance. We can
now redesign our controller. Since we need to place one closed-loop
pole for each pole in the plant, we will place another pole at -300,
which will be faster than the rest of the poles. Since the
closed-loop system matrix depends on Bau, we will use
Bau in the place command rather that Ba. Add the
following to your m-file:
Aa=[0 1 0 0
0 0 1 0
0 0 -b/J K/J
0 0 -K/L -R/L];
Ba=[ -1 ; 0 ; 0 ; 0];
Bau=[0 ; 0 ; 0 ; 1/L ];
Ca=[0 1 0 0];
Da=[0];
p4=-300;
Kc=place(Aa,Bau,[p1,p2,p3,p4]);
t=0:0.001:.05;
step(Aa-Bau*Kc,Ba,Ca,Da,1,t)
Run your m-file (or just these new lines) and you will get the
following output.
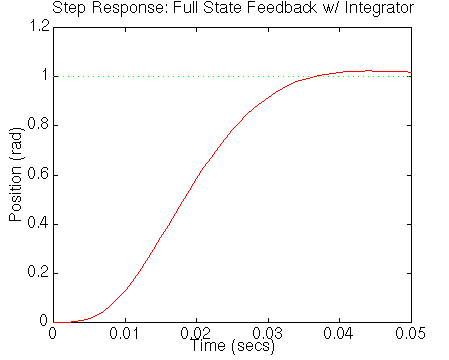
To look at the disturbance response, we apply a similar B matrix as we
did previously when simulating the disturbance response.
step(Aa-Bau*Kc,[0 ; 0 ; 1/J ; 0] ,Ca,Da,1,t)
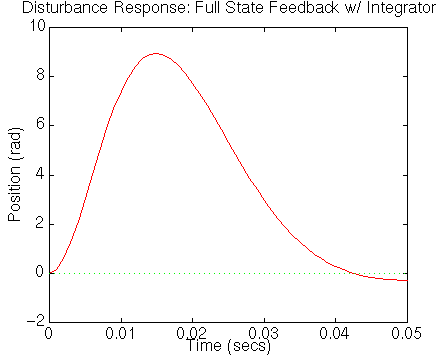
We can see that all of the design specifications have been met by this
controller.
User Feedback
-
State Space Examples
-
Cruise Control |
Motor Speed |
Motor Position |
Bus Suspension |
Inverted Pendulum |
Pitch Controller |
Ball and Beam
-
Motor Position Examples
-
Modeling |
PID |
Root Locus |
Frequency Response |
State Space |
Digital Control:RL
-
Tutorials
-
Basics |
Modeling |
PID |
Root Locus |
Frequency Response |
State Space |
Digital Control |
Examples



8/22/1997 JL
8/24/1997 WM